Viernes, 8 de mayo de 2020

Buenos días, lo primero las soluciones del miércoles. En esas fichas había cosas muy fáciles, otras regulín y algunas difíciles. No pasa nada si hay cosas que no habéis podido hacer, todo eso lo veréis de nuevo el año que viene en el insti. Pero no está mal si habéis estrujado vuestro cerebro matemático en intentar averiguar algunas de esas partes más complicadas. Haced clik en la palabra aquí que tenéis abajo y se os abrirá un documento con las soluciones y explicaciones.

AQUÍ

Por fin es viernes. Para hoy un  poquito de cálculo y juegos online:

Y AQUÍ un juego de perímetros y áreas.

¡Buen finde!

Miércoles, 6 de mayo de 2020

Las soluciones de ayer:

Página 190

Página 191

Buenos días. Vamos a por el miércoles. Hoy problemas de áreas. Leed bien los enunciados y hacedlo más de una vez para comprender bien lo que se nos pide. Ahí van:

No hace falta que los copiéis, los hacéis en la libreta. 

¡Nos vemos el viernes!

Martes, 5 de mayo de 2020

Aquí están las soluciones de ayer....

Página 186

Página 187

Página 188

Página 189

Hoy vamos con los polígonos regulares. En concreto vamos a trabajar con PENTÁGONOS (5 lados) y HEXÁGONOS (6 lados).

Antes de deciros cómo se halla el área de estos polígonos os tengo que hablar del APOTEMA. Y ¿qué es el apotema? Es un segmento que une el centro del polígono con el punto medio del lado. Una imagen para que quede muchísimos más claro:

Bien, pues una vez que sabemos esto, veamos cuál es el área de un polígono regular:

Vamos con un ejemplo:

En este pentágono cuyo lado es 6, como es regular todos sus lados miden lo mismo, y cuyo apotema es 3, el área sería: 

• Primero hallamos el perímetro: ¿Cuántos lados tiene el pentágono? 5. Entonces su perímetro sería:
• 6 cm + 6 cm + 6 cm + 6 cm + 6 cm = 30 cm
• O lo que es lo mismo: 6 cm x 5 lados = 30 cm
• Segundo aplicamos la fórmula, arriba perímetro x apotema:
• 30  x 3  = 90 y 90/2 = 45

El área de este pentágono es 45 cm² 

Yo creo que es fácil, leedlo despacio para no liaros. De todas formas lo tenéis también en la página 190 del libro. ¿Ok?

Seguimos un poquito más: área del CÍRCULO.

Cosas que tenemos que recordar:

• Radio: el radio es el segmento que une el centro del círculo con un punto de la circunferencia. (Acordaos que el radio de la rueda de la bici).
• Y el diámetro: es el segmento que une dos puntos de la circunferencia pasando por el centro. Por lo tanto el diámetro es el doble que el radio. 

• Os acordáis que hablamos del número π (pi), porque era un número con infinitos decimales. π = 3,14159... Vosotros solo tenéis que utilizar las dos primeras cifras decimales, es decir: π = 3,14 ¿vale?
• Ahora tenemos que hablar de la longitud de la circunferencia que se halla con la siguiente fórmula:
• Longitud de la circunferencia = 2 x π x radio. Es decir 2 multiplicado por π y por el radio. Ejemplo: supongamos que el radio del circulo de arriba mide 3 cm ¿Cuál sería la longitud de la circunferencia: 
• L= 2 x π x 3 = 2 x 3,14 x 3 = 18,84
• Ahora vamos a ver como se halla el área.

Veamos un ejemplo: ¿Cuál es área de la círculo de arriba? 

• A= π x r² = 3,14 x 5² = 3,14 x 25 = 78, 5 cm² 

Otra cosa que tenemos que tener en cuenta: y si en vez de tener el dato de la medida del radio tenemos el valor del diámetro.

¿Cómo hallamos el área? El diámetro es el doble del radio ¿verdad? por tanto si el diámetro mide 8, el radio medirá 4. Y con ese dato ya puedo hallar el área. 

Deberes:

Página 190: ejercicio 2.

Página 191: ejercicio 2

Mañana más. ¡Qué tengáis un buen día!

Lunes, 4 de mayo de 2020

Hola chicos, una semana más o una semana menos, según como queráis verlo...

Hoy empezamos con las figuras planas. Esto también es repaso de 5º y lo volveréis a ver en el insti. Así que tranquilos. Es muy fácil.

Lo tenéis todo en el libro (tema 10), pero vamos a verlo aquí uno por uno.

Antes de ir a las figuras os recuerdo lo que es el PERÍMETRO. ¿Qué es? Es la suma de las longitudes de los lados de un polígono. Por ejemplo: 

En el triángulo que tenéis debajo, el perímetro sería 14 cm. ¿De dónde sale ese 14? 5+5+2+2 = 14 cm

En cambio el área es la medida de su superficie, es decir todo lo que esta coloreado en naranja. Las áreas se miden en cualquier unidad al cuadrado. En el caso del triángulo de arriba sería:  

5 cm x 2 cm = 10 cm²

Si fuera en metros tendríamos que: metro x metro = a metro al cuadrado. En notación matemática lo expresamos así: 

m x m = m²

Vamos con las áreas

Empezamos con el triángulo, cuadrado, rectángulo, rombo y romboide.

Fácil ¿no? Base (el lado sobre el que se apoya) x altura

En este caso el área de este triángulo sería 5 x 3 = 15 y 15 : 2 = 7,5 metros.

Un caso especial :

En los triángulos obtusángulos, como el de la imagen de arriba, la altura está fuera del triángulo, pero el área se halla de la misma manera. Se llama triángulo obtusángulo porque tiene un triángulo obtuso (el que está pintado en azul).

ÁREA DEL CUADRADO

Área del cuadrado es igual a lado x lado o lo que es lo mismo lado al cuadrado. Supongamos que en el cuadrado de la imagen su lado vale 4 cm. El área sería 4 x 4 = 16 cm.

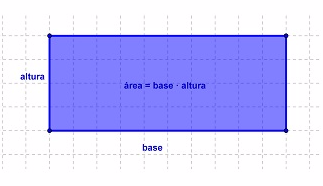
ÁREA DEL RECTÁNGULO

El área del rectángulo es base x altura. Supongamos que en el triángulo que tenéis en la imagen la altura mide 3 cm y la base 5cm. El área sería 3 x 5 = 15 cm.

ÁREA DEL ROMBO

El área del rombo es igual a la DIAGONAL MAYOR (D) por la DIAGONAL MENOR (d), partido por 2. 

Si en el rombo de la imagen D = 6 cm y d=3 cm el área 

 sería 6 x 3 = 18, 18 : 2 = 9 cm. 

ÁREA DEL ROMBOIDE

El área del romboide es base x altura, fijaos bien cual es la altura. 

Creo que es fácil y es todo repaso. Para mañana los siguientes ejercicios:

Página 186: 1.

Página 187: 1 y 2.

Página 188 : 2

Página 189: 2

Las dudas, ya sabéis, a los comentarios (pero decidme quiénes sois)

Besos y abrazos virtuales.

Miércoles, 29 de abril de 2020

Hola queridos alumnos.

Lo primero los resultados del cálculo de ayer:
2735,28 + 935,2 = 3670,48
79372,49 - 155,375 =79217,115
9274,51 x 8,312 = 77089,72712
6274,35 : 105 = 59,75 Resto: 60
96524,28 :7,32 = 13186 Resto: 276
413,24: 517 = 0,79 Resto: 381

Como el viernes es festivo os voy a poner una actividad un poco más divertida. Se trata de juegos (y no, no me refiero al fortnite y eso 😆) Es una página con juegos de todas las asignaturas. Os he buscado uno de porcentajes, a ver qué tal se os da. Os pongo el enlace.

Pinchad AQUÍ (Justo en la palabra)

En el siguiente enlace que os voy a poner podéis encontrar muchos más. Investigad un ratito y a ver cuánta puntuación sois capaces de conseguir... 

AQUÍ

Os dejo un enlace más por si alguno quiere aprender a escribir en el teclado. Sé que había algún alumno o alumna que le gustaría aprender.

Y AQUÍ

Lunes, 27 de abril de 2020

Buenos días a todos. Una semana menos para que llegue el verano.

Lo primero las soluciones del miércoles pasado. Por favor,  corregid lo que tengáis mal y las dudas a los comentarios. (Cuando comentéis decid quién sois, please).

Hoy vamos a hablar de escalas y planos y para ello además de leer la página 172 del libro quiero que veáis este vídeo.

Espero que os haya quedado claro. De deberes hoy vamos a dibujar el plano de una habitación. Vamos a inventar una habitación. 

A continuación os pongo el plano de una  que yo he dibujado. En ella pongo lo que miden los distintos muebles en el plano, vosotros tenéis que averiguar cuánto medirían en la realidad.

La escala es 1:20, eso quiere decir que si yo dibujo 1 cm en la realidad correspondería a 20 cm. Por tanto si dibujo algo de 2 cm en la realidad mediría 40 cm... ¿Lo entendéis? Bien, tenéis que poner lo que miden los distintos muebles: cama, escritorio (por cierto, que me ha salido un escritorio enorme), estanterías, armario y ventana.

¿Os atrevéis a hacer un plano? Podéis hacer vuestra habitación o una inventada... .

Miércoles, 22 de abril de 2020

Buenos días, chicos y chicas.

Lo primero las soluciones de ayer:

Si alguno no entiende los problemas aquí os dejo unos vídeos explicando su resolución.

¿Qué tal con los porcentajes? Fácil, ¿no?

Pues hoy toca practicar problemas de porcentajes. Vais a hacer los ejercicios 1 y 2 de la página 170.

Nos volvemos a ver el viernes. Los jueves no tenemos mates.

Las dudas en los comentarios y si necesitáis que resuelva algún problema porque no lo entendéis me lo decís. ¿Vale?